Dennis' Portfolio

What if we could represent 3D objects not as traditional meshes, but as continuous functions? Signed Distance Functions (SDFs) provide a compact and efficient way to define 3D shapes mathematically. Instead of storing geometry explicitly, an SDF encodes the distance from any point in space to the object’s surface, allowing for smooth interpolation, advanced boolean operations, and real-time rendering.

In this project, I trained a Neural SDF model to learn the implicit representation of a 3D object, converted it into GLSL, and rendered it in real-time using OpenGL ray marching.

This is how I approached the project:

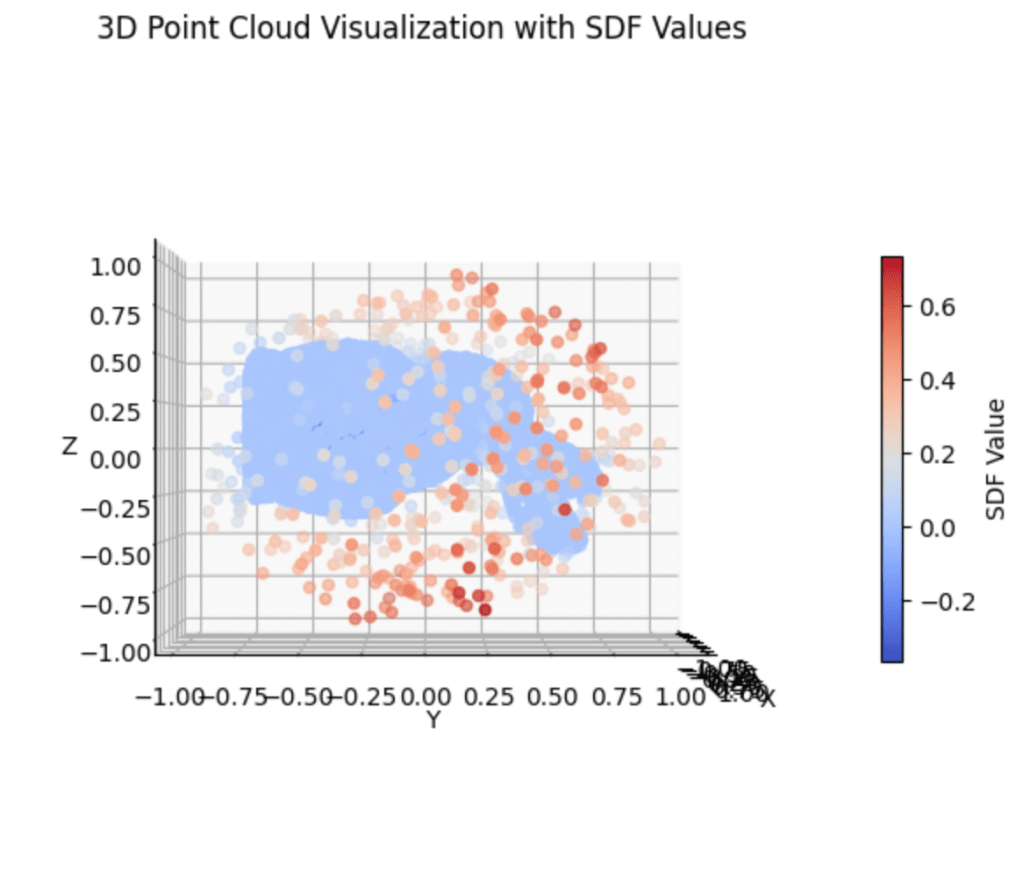
Step 1: Sampling SDF Values from a Mesh

• Loaded a 3D model (.obj) and sampled points near its surface.

• Computed signed distance values (negative = inside, positive = outside).

• Stored the dataset as PyTorch tensors for neural training.

Step 2: Training a Neural SDF Model

• Designed an MLP with sine activations (SIREN) for high-frequency detail.

• Trained on (x, y, z) coordinates -> SDF values using MSE loss.

• The model learns a continuous representation of the object.

Step 3: Converting the Model to GLSL

• Extracted network weights and hardcoded them into GLSL functions.

• Implemented ray marching to evaluate the SDF in an OpenGL fragment shader.

Step 4: Real-Time Rendering with Ray Marching

• Cast camera rays, iteratively sampled the SDF, and stopped at surface hits.

• Computed normals via finite differences for shading.

• Applied Phong shading for a realistic look.